Сорок седьмая проблема Евклида, более широко известная как Теорема Пифагора, довольно часто упоминается в Масонских текстах. Общее объяснение, которое даётся значению сорок седьмой проблемы Евклида в Масонстве присутствует в Лекции Третьего Градуса и гласит следующее: «Она является Масонским символом, который учит Масонов любить науки и искусства». Это объяснение является выборкой из статьи, опубликованной в Масонском журнале «Иллюстрация Масонства» издания 1797 года, автором которой является основатель Йоркского Устава Томасом Уэбб. Эта статья включает в себя следующий параграф:
«Сорок седьмая проблема Евклида является изобретением его старшего друга и брата, великого Пифагора, который во время своих путешествий по Азии, Африки и Европе был посвящен в несколько жреческих орденов, а также посвящен в Возвышенный Градус Мастера. Этот мудрейший из философов обогатился знанием практически всех наук своего времени, но особенно преуспел в геометрии, или масонстве. В этой области знания он вывел множество аксиом и доказал множество теорем, среди самых знаменитых из которых – эта, доказав которую он в сердечной радости вскричал «Эврика!», что по-гречески означает «Нашел!», а после этого приказал принесли гекатомбу. Она учит масонов любить знания и науки».
Несмотря на кажущиеся несостыковки с современным виденьем истории философии, это объяснение продолжает использоваться и в наши дни. Упоминается сорок седьмая проблема Евклида и в «Книге Мастера», написанной Карлом Гарри Клауди в начале 20-го века. Про сорок седьмую проблему Евклида там написано следующее:
«За исключением Всевидящего Ока, данная эмблема наполнена самым глубоким смыслом из всех символов Возвышенного Градуса. Однако чаще всего ей уделяют меньше внимания, чем прочим эмблемам, а понимают еще меньше.»
Графическое изображение сорок седьмой проблемы Евклида также является символом Бывшего Досточтимого Мастера Ложи.
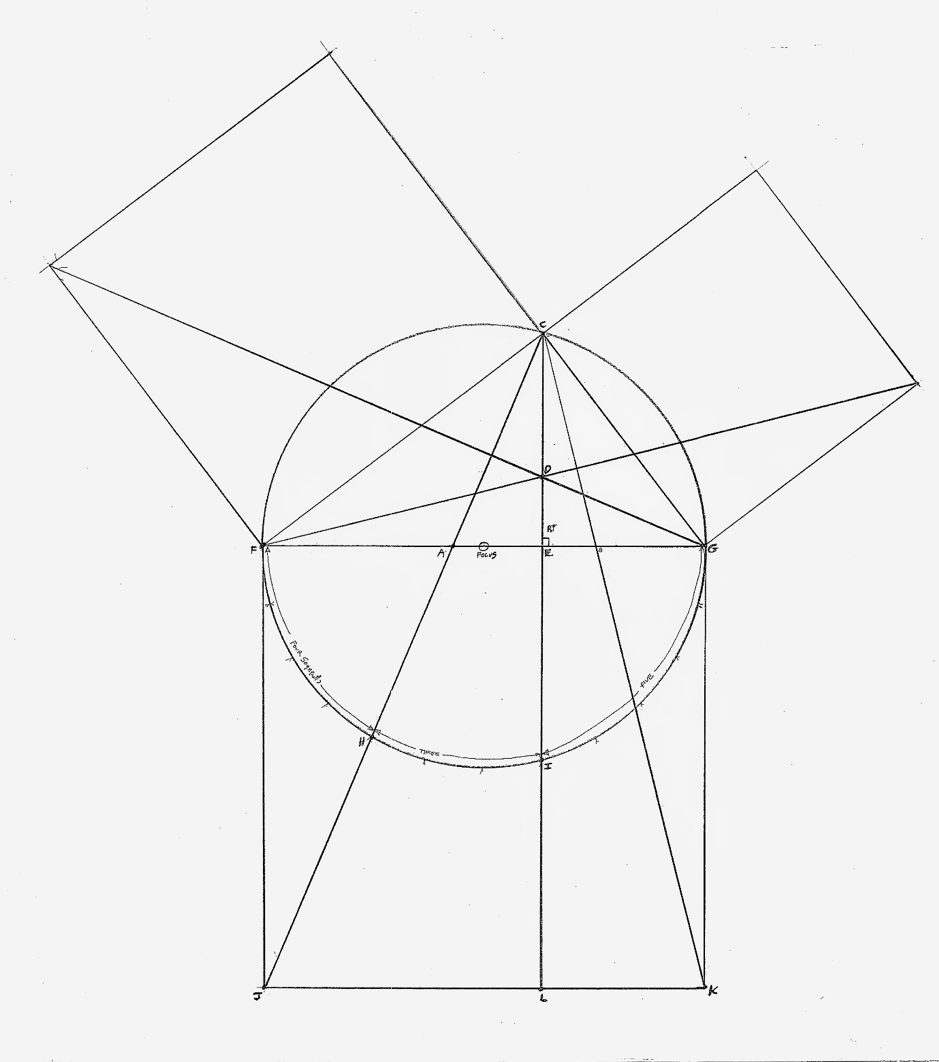
Так каковы же причины столь высокой значимости решения Теоремы Пифагора в Масонстве? Почему эта простая формула: A2 + B2 = C2 и её графическое отображение имеют столь высокую важность?
В Древних Конституциях средневековых оперативных масонов Геометрия зачастую отождествлялась с Масонством. Геометрии выделено особое место и в Конституции Андерсона — слово «Геометрия» в ней повторяется тридцать три раза. В первом параграфе Конституции Андерсон пишет:
«Адам, первый предок наш, сотворенный по Образу и по Подобию Бога — Великого Архитектора Вселенной — определенно имел Вольные Науки, в особенности Геометрию, начертанными в самом сердце своем, ибо с самого времени Грехопадения зрим мы первоосновы ее начертанными в сердцах потомков его, а Время постепенно превратило ее в удобный метод изучения предположений посредством соблюдения Законов Соответствия, взятых из Механики. Таким образом, Механистические Науки дали ученым повод свести элементы Геометрии к методу, и сия достойная Наука, таким методом суженная, легла в основание всех искусств (в особенности Каменщичества) и стала законом, посредством коего все они управляются и работают».
Важность того, что с параграфа о геометрии начинается один из самых важных документов в Масонстве, и ещё в столь фундаментальном контексте нельзя переоценить. Упоминает Конституция Андерсона и Евклида. Про Евклида, в Конституции написано:
«Нет нужды сомневаться в том, что и Каменщичество шло бок о бок с Геометрией, а точнее соразмерно следовало ей на всех этапах постепенного развития вплоть до того времени, когда в Александрии расцвела школа Эвклида Тирского, собравшего вместе рассеянные по миру Элементы Геометрии, и переработавшего их в единый Метод…»
Для Масонов, Геометрия — это наука, которая является основой познания мира, и одним из семи свободных искусств (Грамматика, Логика, Риторика, Арифметика, Музыка, Геометрия и Астрономия) изучение которых является неотъемлемой частью Масонства. Чтобы понять значение сорок седьмой проблемы Евклида в Масонстве, необходимо знать каково её значение в геометрии, философии, арифметике и музыке, каково её практическое применение, каково её место в античной философии, и кем были Пифагор и Евклид.
Пифагор Самосский, древнегреческий философ, живший в VI веке до нашей эры. Его имя известно практически всем из-за теоремы Пифагора, которая входит в школьную программу по геометрии. Пифагор был первым мыслителем, который по преданию назвал себя философом, то есть «любителем мудрости». Он же впервые назвал вселенную космосом, то есть «прекрасным порядком». Предметом его учения был мир как стройное целое, подчиненное законам гармонии и числа. Он является открывателем Пифагорова строя в музыке, при котором соотношения частот всех интервалов основаны на соотношении 3:2. Он был одним из первых кто увидел в музыкальных гармониях математические основы.
Последователи Пифагора делились на слушателей и математиков. Слушатели (или Акусматики) имели дело с религиозными и ритуальными сторонами учения, математики — с исследованиями четырёх пифагорейских «матем»: арифметики, геометрии, гармоники и астрономии. Акустиматикам было запрещено смотреть на Пифагора, и он преподавал им из-за занавеса. Это было для них уроком того, что необходимо поднять своё развитие до определённого уровня, прежде чем получить возможность получать знания и мудрость напрямую от Пифагора.
Последователи Пифагора следовали строгому этическому коду, положения которого часто были выражены в криптических аллегориях. Все Пифагорейцы были вегетарианцами, так как верили в реинкарнацию. Основным правилом в Пифагорействе была эхемифия – запрет говорить если ты сомневаешься. По сути, Пифагорейцы являлись, во многом, аналогом спекулятивного Масонства в Древней Греции, и поэтому не удивительно что Уэбб называет Пифагора Мастером Масоном.
Авторство теоремы Пифагора не принадлежит самому Пифагору. Доподлинно известно, что решение этой проблемы знали ещё в Древнем Египте. В древности это называлось «Египетский трюк с верёвкой». Есть предположение что этот «трюк» использовали при построении пирамид, для определения прямых углов. Сделать это довольно просто – берётся верёвка, на ней вяжутся узлы на равных расстояниях друг от друга. При помощи верёвки делается треугольник, со сторонами 3,4 и 5 узлов. Получается прямоугольный треугольник — 32 + 42 = 52 (9 + 16 = 25).
Доказательство теоремы в исполнении самого Пифагора не дошло до наших дней, однако именно так называет Евклид эту теорему в первой книге своего тринадцати томного труда «Начала». По сути, это сборник, где при помощи логики к решаются геометрические задачи. Эта работа Евклида является основой той части современной Геометрии, которую в наше время называют «Евклидовой». Евклид жил в Древней Греции в III веке до нашей эры, был учеником Платона. Его «Начала» входили в коллекцию легендарной Александрийской Библиотеки. Книги с таким же названием, в которых последовательно излагались все основные факты геометрии и теоретической арифметики, составлялись ранее Гиппократом Хиосским, Леонтом и Февдием. Однако «Начала» Евклида вытеснили все эти сочинения из обихода и в течение более чем двух тысячелетий оставались базовым учебником геометрии. Создавая свой учебник, Евклид включил в него многое из того, что было создано его предшественниками, обработав этот материал и сведя его воедино. В создании и развитии науки Нового времени «Начала» сыграли важную идейную роль. Они оставались образцом математического трактата, строго и систематически излагающего основные положения той или иной математической науки.
Сорок седьмая проблема Евклида и её решения применяются в архитектуре, астрономии, навигации, строительстве, инженерии и многих других сферах деятельности человека. С её помощью можно определить по звёздам своё местоположение в открытом море, рассчитать время следующего прилива или солнечного затмения. Она является символом мудрости и знаний и является одной из основ современной науки. С её помощью мы можем смотреть на вселенную, вооружившись знанием и делать о ней суждения, основанные на логике.
В Масонстве, некоторые Ложи используют сорок седьмую проблему Евклида в убранстве Храма. С помощью её Ложа принимает правильную форму, определяются места для светочей Ложи, свечей, колонн и других предметов убранства Ложи. В Масонских ритуалах, количество странствий в разных градусах определяется соотношением 3:4:5, что соотносится с практическим применением решения сорок седьмой проблемы Евклида, используемым в прошлом строителями пирамид и средневековых соборов. Также можно рассматривать формулу А2 +В2 = С2 как символ взаимодействия и взаимоотношений между тремя градусами Символических Лож. Считается что графическое изображение Теоремы Пифагора является символом Бывшего Досточтимого Мастера потому, что она является символом полноты знаний, и пройдя путь от ученика до Досточтимого Мастера, а затем выполнив свою работу, которая требует много знаний и мудрости, человек становится более совершенным в своём развитии. Этот очень важный Масонский символ имеет огромное количество трактовок и значений, основанных на Геометрии, символизме и философии, на познание которых может уйти вся жизнь.



